摘要
互联网的持续爆发式扩张极大的增加了采用推荐系统过滤大量的信息的必要性,推荐系统被社会学,计算学物理学家和交叉学科等大量学界进行了广泛的研究 ,尽管取得了实质性的理论和实践成果,缺乏统一方法对不同的推荐算法比较,阻碍了其进一步的进步。在本文中,我们回顾了推荐系统的最新进展,并讨论了主要挑战。我们对比并评估了已有的算法,并推测他们在未来的发展中扮演的角色。除了算法之外,我们还从物理的角度来描述推荐系统的宏观行为。我们讨论了推荐系统潜在的影响和未来的发展。我们在此强调:推荐系统有很强的科学深度并结合了不同的研究领域,吸引着物理学家以及交叉学科研究人员的兴趣。
序言
由于计算机和计算机网络,我们的社会各方面都经历着翻天覆地的变化,我们在线购物,通过搜索引擎搜集信息,在互联网上进行很大部分的社会活动。事实上,我们大量的行为和交互都以电子的方式存储,这给了研究人员机会在更加细尺度来研究社会经济和技术社会系统,传统的“软学科”,比如社会学和经济学,通过对这些已有的新数据的研究已经发展了许许多多的研究分支,在数据驱动研究方面有着长期经验的物理学家,也已经加入了这一趋势,为诸如金融[3,4],网络理论[5-9]和社会动力学[10]等多个非传统领域做出了贡献。随着过去十几年间物理学家的兴趣的持续增长,推荐系统和信息检索的研究也不例外。推荐系统的任务是利用用户及其偏好的数据预测用户未来可能的喜好和兴趣。推荐系统的研究处于科学和社会经济生活的十字路口,其巨大的潜力首先被信息革命前沿的网络企业家所注意。虽然原本是由计算机科学家主导的领域,但推荐系统需要各领域的贡献,现在它也是数学家,物理学家和心理学家感兴趣的话题。例如,最近在商业公司Netflix [11]组织的的推荐比赛中,基于人类行为的心理学方法获得高分并不是巧合。
当为目标用户做推荐时,最基本的方法是选择与目标用户相似的用户所青睐的对象。即使这种简单的方法也可以通过多种方式实现,这是因为推荐领域缺乏一般性的“第一原则”-从中可以推断出正确的推荐方式。例如,如何最好地衡量用户相似性并评估其不确定性?如何综合各种用户的意见分歧?如何处理少量信息的用户?所有数据是否权重平等,或者是否可以检测到鲁莽或故意误导的意见?当使用比基于用户相似性的方法更复杂的方法时,也出现和这些类似的问题。幸运的是,存在一些可用于测量和比较各种方法的实际数据集。因此,与物理学类似,实验决定哪种推荐方法是好的,哪种不是。
认为推荐系统只有在适当的数据集可用的情况下才会被研究是非常有误导性的。虽然数据的可用性对推荐方法的实证评估很重要,但主要驱动力来自实践:电子系统给我们太多的选择让我们自己来处理。工业界对推荐的兴趣并不奇怪,一本关于推荐系统领域的早期书《Net Worth by John Hagel III and Marc Singer [12]》明确指出“(info-mediaries)”的巨大经济影响,它可以大大提高个人消费者的信息能力。现在,大多数电子商务网站提供各种形式的推荐–从简单的显示最受欢迎的项目或通过复杂的数据挖掘技术推荐的相同生产者的其他产品。人们很快意识到没有独特的最佳推荐方法, 相反,根据可用数据的上下文和密度,对不同的应用场景采用不同的推荐算法是最有可能成功的。因此,没有灵丹妙药,最好的办法是了解基本的前提(推荐场景)和推荐机制,这样就可以解决来自生活中的各种真实应用问题。 这一点也反映在这篇综述中,我们不试图强调任何推荐算法。 相反,我们回顾基本的思想,方法和工具with particular emphasis on physics-rooted approaches.
撰写此综述的原因是多方面的,首先,虽然计算机科学家对推荐系统的广泛评论已经存在[13-15],但是物理学家与计算机科学家的观点不同,它们更多的使用复杂网络方法和采用各种经典物理过程(如扩散)来做信息检索。因此,我们相信,该综述(We thus believe that this review with its structure and emphasis on respective topics can provide a novel point of view.)可以提供一个新颖的观点。 其次,过去十年已经看到物理学家对推荐系统的兴趣越来越大,我们希望通过用物理学界更熟悉的语言来描述最先进的技术的这篇综述可以成为他们的有用来源。 最后,这里介绍的跨学科方法可能为信息检索领域的开放性问题和挑战提供新的见解和解决方案。
本篇综述结构如下:为了激发研究问题的积极性,我们首先在第2章讨论了推荐系统的实际应用。接着在第3节中,我们介绍了基本概念,例如复杂网络,推荐系统和评估指标,这些概念构成了后续阐述的基础。 然后,我们开始讨论推荐算法,首先是传统方法(第4节中基于相似性的方法和第5节中的维数降低技术),然后是起源于随机游走过程被物理学所熟知的基于网络的方法(在第6节)。还包括基于外部信息的方法,如社交关系(第7节),关键字或时间戳(第8节)。 我们最后在第9节中对推荐算法的性能进行简要评估,并在第10节讨论了该领域的前景。
推荐系统应用真实场景
Netflix prize
主要挑战
推荐系统领域的研究人员面临着许多挑战,这些挑战对其使用和执行算法构成风险。这里我们只提到主要的:
数据稀疏 由于可用数据量非常大(比如,大型的在线书店经常有几百万的书),导致用户之间的交集十分小甚至没有。此外,即便每个用户/商品平均评估次数很高,但是由于每个商品/用户的评估次数分布非常不均匀(通常是power-law或者weibull分布),大部分的商品只有极少的评分,所以一个有效的推荐系统必须考虑到数据的稀疏性问题。
可扩展性 尽管数据经常是稀疏的,但是对于那些大型的网站拥有百万的用户和商品。因此必须考虑计算成本的问题,寻找计算要求不高的或者易于并行化的推荐算法。另一种可能的解决方案是基于使用增量数据的算法(增量学习算法),随着数据的增长,算法不会在全局重新计算,而是逐步增量计算[29,30],这种增量方法类似于在物理和数学广泛应用的扰动技术[31]。
冷启动 当新的用户进入一个系统,系统中没有任何有用的信息来产生推荐结果给用户,通常的解决办法是通过结合基于内容的和协同过滤的混合推荐技术(参考 8.4 节),有时还需要获取用户的一些基本信息(如年龄,位置和偏好等)来配合。另外的一个方法是识别不同web服务中的同一个用户。比如说百分点开发了一个可以跟踪同一个用户在不通电商网站行为的技术,那么一个在A网站作为冷启动的用户可以通过他在B,C,D 网站的行为来进行相关的推荐。
多样性与精确性的两难困境 当推荐任务是为特定用户赞赏的项目时,通常最有效的方法是推荐流行的和高评分的项目,但是这样的推荐对用户来说没有什么价值,因为即便在没有推荐系统的情况下,流向的项目也很容易被找到(甚至难以避免),因此一个好的推荐项目列表也应该包括那些用户自己本身无法找到的隐藏项目[35]。对于这个问题的解决办法有:直接增加推荐列表的多样性[36-38]和使用混合的推荐算法[39]
攻击的脆弱性 受推荐系统在电子商务领域重大的经济利益的驱动,一些心怀不轨的用户通过提供一些虚假恶意的信息,故意增加或者压制某些商品被推荐的可能性[44]。从阻止恶意评估进入系统到复杂的抵抗推荐技术[41],有大量的工具可以防止这样的行为。然而,这并不是一件容易的事情,因为随着防作弊的工具的升级,攻击者的策略也越来越先进。例如,Burke等人[42]引入了八个攻击策略,进一步可以分为四个类:基本攻击(包括随机和平均攻击),低认知攻击,核攻击和知情攻击。(basic attack, low-acknowledge attack, nuke attack and informed attack.需要看引文来翻译)
时间的价值(好像是讲兴趣漂移问题) 一个真实用户的兴趣是和时间尺度相关的(举例来说,短期感兴趣与旅行计划相关,长期兴趣和居住地或者政治相关),大多数的推荐算法评估的时候都忽略了时间的影响。旧的想法是否会随着时间衰减,怎么衰减,以及用户评估和项目相关性中的典型临时模式是什么,这些都还需要持续的研究
推荐的评估 虽然我们有很多不同的指标(见第3.4节),但是如何根据给定的情况和任务选择最好的指标仍然是一个悬而未决的问题。不同推荐算法的比较也存在问题的,因为不同的算法可以简单地解决不同的任务,最后,推荐系统的整体用户体验(包括用户对推荐结果的满意程度和用户对系统的信任)难以在“离线”评估中进行测量。因此,在推荐系统中,实证用户的研究仍然是一个受欢迎的反馈来源。
用户界面 实践表明,为了促进用户接受推荐结果,推荐过程需要透明化:用户明白为什么特定的项目被推荐给他们。除此之外,通常潜在的感兴趣项目列表会很长,因此它需要简单的方式来展现,并且可以轻松的通过他去浏览由不同方法给出的推荐结果。
除了以上的长期挑战,推荐系统近期出现了许多新颖的问题,由于相关科学的方法论的发展,特别是网络分析的新工具,科学家开始考虑网络结构对推荐的影响,以及如何利用已知的结构特征来改进推荐。例如,Huang等人[47]分析了消费者-商品网络,并提出了一种改进的推荐算法,这种算法偏向增强局部聚类属性的边。Sahebi等[48]设计了一种利用社区结构的改进算法。新技术的进步和传播也带来新的挑战。例如,配备GPS的手机已经成为主流,互联网的被普遍的接入,因此基于位置的推荐现在是可行的并且越来越显有意义,精准的推荐要求人类的运动的高可预测性和定量方式来定义地点和人之间的相似之处。最后,智能推荐系统应考虑不同人群的不同行为模式。例如,新用户倾向于访问非常受欢迎的项目并选择类似的项目,而老用户通常具有更具体的兴趣[53,54],并且用户在低风险(例如收集书签,下载音乐等)和高风险(例如购买电脑,租房等)活动之间的行为差异很大。
其实可以直接看周涛老师的一篇中文论文 《个性化推荐的十大挑战》,里面讲的更加具体,虽然推荐系统经过了这么多年的发展,但是对现在的推荐系统依旧面临着文中的问题。
主题和问题的定义
我们在本章中简要回顾一下在推荐系统研究中有用的基本概念。
1. 图
网络分析是揭示许多复杂系统组织原理的通用工具[5-9]。网络是一组元素(称为节点或顶点),它们之间具有连接(称为边或链接)。许多社会,生物,技术和信息系统可以被描述为具有代表个人或组织的节点和捕获其交互的边缘的网络。 网络研究,即数学文献中的图论,具有悠久的历史,从18世纪欧拉所解决的古典柯尼斯堡桥梁问题开始[57]。用数学的定义,网络\(G\)是一个有序的不相交的二元组集合\((V,E)\)其中\(V\)是节点的集合\(E\)是边的集合。在一个无向网络中,一条连接节点\(x\)和\(y\)的边表示为\(x \leftrightarrow y\),\(x \leftrightarrow y\)和\(y \leftrightarrow x\)代表的是同一条边,在一个有向网络中,边是一个关于节点的有序二元组,\(x\rightarrow y\) 代表由\(x\)指向\(y\)的一条边,边\(x\rightarrow y\) 和\(y\rightarrow x\)是不同的,并且可以同时存在的。除非另有说明,否则我们假设网络不包含自环(连接节点到其自身的“边”)或连接同一对节点的多边(多个“边”)。在多网络(multinetwork)中,允许两个循环和多边。
在无向网络\(G(V,E)\)中,如果\(x\leftrightarrow y \in E\),则两个节点\(x\)和\(y\)被认为是彼此相邻的。节点\(x\)的邻域节点集合,或者说\(x\)邻居集合由\(\Gamma_{x}\)来表示,节点\(x\)的度定义为\(k_{x}=|\Gamma_{x}|\).度分布\(P(k)\)定义为随机选择的节点的度为\(k\)的概率.在一个均匀的网站,每一个节点有着相同的度\(k_{0}\),所\(P_{k}=\delta_{k,k_{0}}\),在经典的Erdös–Rényi随机网络中,其中每对节点以给定的概率\(p\)连接生产边,其度分布满足二项式分布。\[P(k)={N-1 \choose k}p^{k}(1-p)^{n-1-k} \quad \quad \quad (1)\]其中\(N=|V|\)是网络中节点的数量。这样的分布有一个以平均度\(\bar x = p(N-1)\)表示的特征量表.在上个世纪末,研究人员转而对大规模实际网络进行调查,结果发现他们的度分布通常跨越几个数量级,大致遵循幂律形式\[P(k)\sim k^{-\gamma} \quad \quad \quad (2) \]其中\(\gamma\)为正指数,通常位于2和3之间[5],这种网络被称为无标度网络,因为他们缺乏度的特征尺度,幂律函数\(P(k)\)是与规模无关的。注意,实践数据中的幂律分布的检测需要固定的统计工具[62,63]。 对于有向网络,由\(k^{out}\)表示的节点\(x\)的出度,是从x开始的边的数量,入度\(k^{in}\)是以x结束的边的数量。 有向网络的进度和出度分布通常彼此不同。
一般来说,如果一个网络的高度节点倾向于与高度节点连接,而低度节点倾向于与低度节点连接,那么它被认为是同配assortative的(如果情况相反,那就是异配的)。 该度-度相关性可以由最近邻节点门的平均度[64,65]或皮尔逊系数的变体称为分类系数[66,67]来表征。 分类系数\(r\)在\(-1≤r≤1\)的范围内。如果\(r> 0\),网络是同配的; 如果\(r <0\),则网络是异配的。 请注意,该系数对度非均匀性(heterogeneous degree )敏感。 例如,无论网络的连接模式如何,r在具有非常非均匀性度分布的网络(例如,因特网)中将为负值[68]。
连接两个节点的路径中的边数被称为路径的长度,两个节点之间的距离被定义为连接它们的最短路径的长度。 网络的直径是所有节点对之间的最大距离,平均距离是所有节点对上的平均距离平均值\[\bar d = \frac{1}{N(N-1)}\sum_{x \neq y}d_{x,y} \quad \quad \quad (3) \]其中\(d_{x,y}\)是\(x\)和\(y\)之间的距离.许多真实网络显示出所谓的小世界现象:它们的平均距离不会比网络大小的对数增长得快[70,71]。
三元聚类在社会互动系统中的重要性的认知已经超过100多年[72]。 在社交网络分析中[73],这种聚类称为传递性,定义为网络中三角形总数与相连节点的三元组总数之比的三倍。 1998年,Watts和Strogatz [71]提出了一个类似的指数来量化三元聚类,称为聚类系数。 对于给定的节点\(x\),该系数被定义为\(x\)的邻居之间边的数量与邻居对的数量的比率,\[c_x=\frac{e_x}{\frac{1}{2}k_x(k_x)-1} \quad \quad \quad (4) \]其中\(e_x\)表示节点\(x\)的\(k_x\)个邻居之间的边数量(该定义仅在\(k_x> 1\)时有意义)。 网络聚类系数被定义为\(k_x> 1\)的所有\(x\)的\(c_x\)的平均值。也可以将聚类系数定义为网络中三角形数\(\times 3\)与连接的三元组顶点数之比,有时也被称为“传递三元组的分数(‘fraction of transitive triples’)”[7]。 请注意,这两个定义可以给出完全不同的结果。
图1说明了简单无向网络的上述定义。 有关网络测量的更多信息,我们鼓励读者去参考关于网络特征的文章[74]。
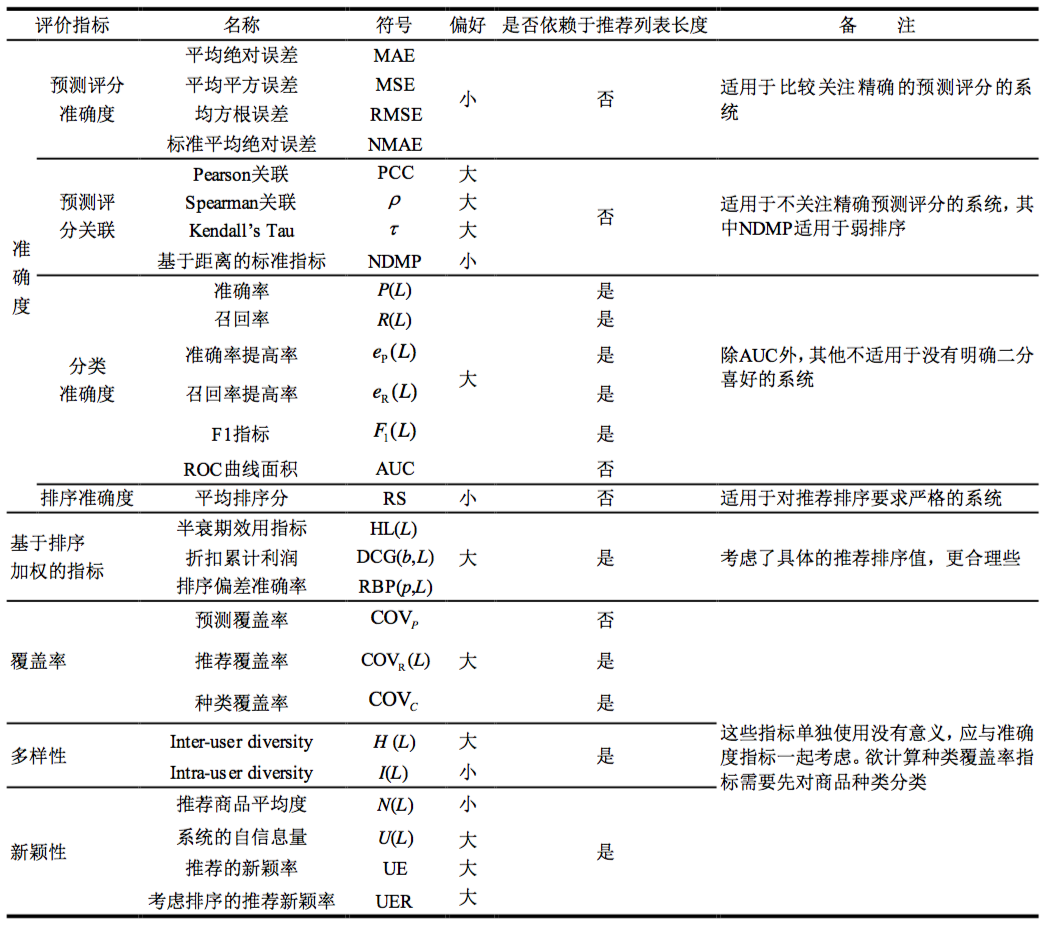
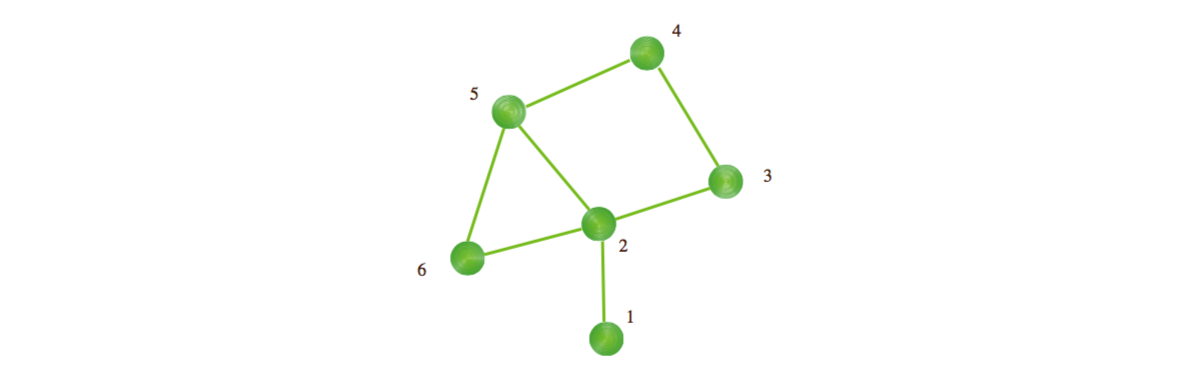 图1. 一个拥有6个节点7条边的简单无向网络,节点的度分别为\(k_1=1,k_2=k_5=3,k_3=k_4=k_6=2\),对应的节点的度分布\(p(1)=\frac{1}{6},p(2)=\frac{1}{2},p(3)=\frac{1}{3}\),网络的直径和平均平均距离为\(d_{max}=3,d=1.6\),聚类系数为\(c_2=\frac{1}{6},c_3=c_4=0,c_5=\frac{1}{3},c_6=1\),平均聚类系数为\(C=0.3\)
图1. 一个拥有6个节点7条边的简单无向网络,节点的度分别为\(k_1=1,k_2=k_5=3,k_3=k_4=k_6=2\),对应的节点的度分布\(p(1)=\frac{1}{6},p(2)=\frac{1}{2},p(3)=\frac{1}{3}\),网络的直径和平均平均距离为\(d_{max}=3,d=1.6\),聚类系数为\(c_2=\frac{1}{6},c_3=c_4=0,c_5=\frac{1}{3},c_6=1\),平均聚类系数为\(C=0.3\)
2. 二部图和超图
如果一个网络\(G(V,E)\)满足分割为\((V_1,V_2)\)后,\(V_1\cup V_2=V\)并且\(V_1\cap V_2=\emptyset\),每一条边由一个\(V_1\)和一个\(V_2\)中的节点连接而成,那么这就是一个二部图。许多真实系统自然地被模拟为二部图,比如,由化学物质和化学反应组成的代谢网络[75],由行为和行为者组成的协作网络[76],由个人电脑和电话号码[77]的互联网电话网络等等。我们专注于一类特殊的二分网络,称为基于网络的用户商品网络[53],它们代表在线服务网站中的用户和商品之间的相互影响,例如在Delicious.com中的书签集合以及在amazon.com上购买的书籍。我们将在后面看到,这些网络描述了推荐系统的基本结构。 基于Web的用户商品网络是逐渐演进的,其中节点和链接逐渐被添加。 相比之下,这不可能发生在例如作者合作网络(例如,在发布之后无法将作者添加到科学论文)。
大多数的基于web的用户商品网络有着共同的结构属性,他们的(object-degree)商品度分布遵循幂律式形式$P(k)k^{-} $,对于互联网电影数据库(IMDb)来说 \(\gamma \approx 1.6\)[78],音乐共享站点audioscrobbler.com的 \(\gamma \approx 1.8\) [79],对于电子商务网站amazon.com [53] \(\gamma \approx 2.3\);对于书签共享网站delicious.com来说 \(\gamma \approx 2.5\)。用户度分布的形式通常在指数和幂律之间[53],并且可以很好地拟合Weibull分布分布[27](文献中也称为拉伸指数分布[80])\[P(k)=k^{\mu-1}exp[-(k/k_0)^\mu] \quad \quad \quad (5) \]其中\(k_0\)是常数,\(\mu\)是拉伸指数。 用户和商品之间的连接(边)表现出一种异配(disassortative)混合模式[53,78]。 二部图定义的简单扩展是所谓的多部图。对于一个r-partite的图,他存在r个节点集合\(V_1,V_2...V_r\),并\(V=V_1 \cup V_2 \cup...\cup V_r,V_i\cap V_j=\emptyset ,其中i\neq j\),并且对于所有的节点集合\(V_i\),不存在同一集合的节点之间的边。多部网络已经在协作标签系统(文献也称众分类法Folksonomies)[81-84]中找到了应用,用户可以在其中为在线资源分配标签,例如flickr.com中的照片,CiteULike.com中的参考文献和delicious.com中的书签等在线资源分配标签。
请注意,三部网络表示形式中丢失了一些信息。例如,给定一条连接资源和标签的边,我们不知道哪个用户(或用户们)对此边有贡献。对于这个问题,超图[85]可以用来给出协作标签系统的完整结构的精确表示。在超图\(H(V,E)\)中,超集\(E\)是\(V\)的幂集的子集,即V的所有子集的集合。 因此,边\(e\)可以连接多个节点。 类似于普通网络,超图中的节点度被定义为与节点相邻的超节点的数量,并且两个节点之间的距离被定义为连接这些节点的最小数量的超边。 聚类系数[82,86]和社区结构[86,87]也可以按照普通网络中的定义进行定义和量化。 请注意,超图和二分网络之间存在一对一的对应关系。给定超图\(H(V,E)\),相应的二分网络\(G(V^\prime,E^\prime)\)包含两个节点集,如\(V^\prime= V\cup E\),而\(x \in V\)与\(Y \in E\)连接,当且仅当\(x \in Y\)(参见图2作为说明)。
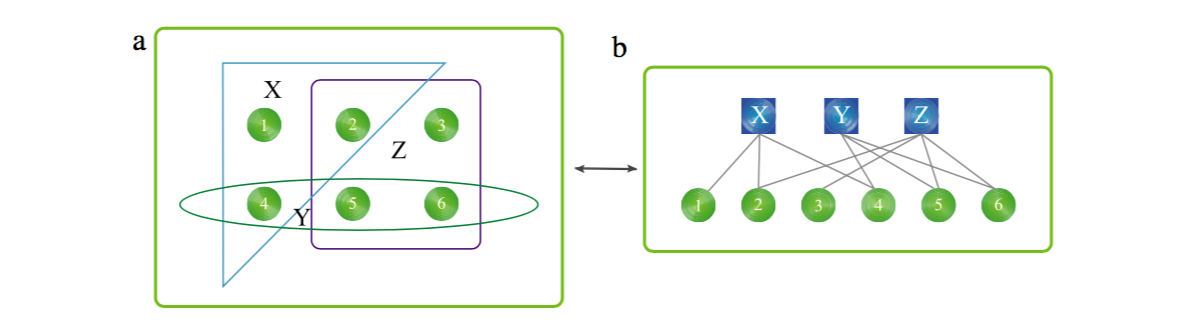 图2. 超图(a)和二分网络(b)之间的一一对应的图示。 有三个超边,X = {1,2,4},Y = {4,5,6}和Z = {2,3,5,6}。
图2. 超图(a)和二分网络(b)之间的一一对应的图示。 有三个超边,X = {1,2,4},Y = {4,5,6}和Z = {2,3,5,6}。
超图已经在铁磁动力学[88,89],人口分层[90],蜂窝网络[91],学术团队形成[92]等许多领域中得到应用。 在这里,我们更关心协作标签系统的超图表示[86,93,94],其中每个超边连接三个节点(由图3中的三角形表示),用户 \(u\) ,资源 \(r\) 和标签 \(t\) , 表示用户 \(u\) 把标签 \(t\) 给了资源 \(r\) 。 资源可以由许多用户收集,并且由用户给出几个标签,标签可以与许多资源相关联,这就导致了小世界超图[86,94](图3显示了基本单元和广泛的描述)此外,协同标签系统的超图已被证明是高度集群化的,它具有长尾度分布和社区结构[86,94]。[94]可以找到超图的演变模型。
 图3. 协同标签网络的超图。 (左)一个类似三角形的超边[93],其中包含三种类型的顶点,一个蓝色圆圈,一个绿色矩形和一个棕色三角形,分别表示用户,资源和标签。 (右)描述由两个用户组成,四个资源和三个标签的超图。 以用户\(U_2\)和资源\(R_1\)为例,测量值表示为:(i)\(U_2\)已经参与在六个超边,这意味着它的超度是6; (ii)\(U_2\)直接连接到三个资源和三个标签。 按照公式 (6),认为它最大可能有\(3 * 3 = 9\) 超边。 因此,其聚类系数等于\(6/9=0.667\),其中6是其超度; 相对而言,如定义按式(7),其聚类系数为\(D_h(U2)= \frac {12-6} {6-4} = 0.75\); (iii)从\(U_2\)到\(R_1\)的最短路径为\(U_2-T_1-R_1\),表示\(U2\)与\(R_1\)之间的距离为2
图3. 协同标签网络的超图。 (左)一个类似三角形的超边[93],其中包含三种类型的顶点,一个蓝色圆圈,一个绿色矩形和一个棕色三角形,分别表示用户,资源和标签。 (右)描述由两个用户组成,四个资源和三个标签的超图。 以用户\(U_2\)和资源\(R_1\)为例,测量值表示为:(i)\(U_2\)已经参与在六个超边,这意味着它的超度是6; (ii)\(U_2\)直接连接到三个资源和三个标签。 按照公式 (6),认为它最大可能有\(3 * 3 = 9\) 超边。 因此,其聚类系数等于\(6/9=0.667\),其中6是其超度; 相对而言,如定义按式(7),其聚类系数为\(D_h(U2)= \frac {12-6} {6-4} = 0.75\); (iii)从\(U_2\)到\(R_1\)的最短路径为\(U_2-T_1-R_1\),表示\(U2\)与\(R_1\)之间的距离为2
一般来说,以复杂科学角度的评估超图可以从以下几点展开(图3给出这些的详细描述):
- 超度:超图中的节点的度可以自然地定义为与其相邻的超边的数量。
- 超度分布:定义为每个超度占据的比例,其中超度定义为常规节点参与的超边的数量。
聚类系数:定义为节点的实际超边数量与可能的超边数量的比例[82]。 例如,用户的聚类系数\(C_u\)定义为\[C_u=\frac{k_0}{R_uT_u} \quad \quad \quad (6)\]其中\(k_u\)是用户\(u\)的超度,\(R_u\)是用户\(u\)收集的资源的数量,\(T_u\)是用户\(u\)拥有的标签的数量。一个较大的\(C_u\)表示你有更相似的资源主题,这也可能表明你更专注于个性化或特殊的话题,而较小的\(C_u\)可能表明他/他有更多的兴趣。也可以用类似的定义来衡量资源和标签的聚类系数。 Zlati¢等人提出了一种名为超边密度的指标[86]。以用户节点\(u\)为例,它们将\(u\)的协调数(the coordination number)定义为 \(z(u)= R_u + T_u\)。对于一个给定的\(k(u)\),配对数最大为 \(Z_{max}(u)=2K(u)\) ,对于 \(n(n-1)<k(u)<n^2\) 情况最小值是 \(Z_{min}(u)=2n\) ,对于 \(n^2<k(u)<n(n+1)\) 情况最小值是 \(Z_{min}(u)=2n+1\) ,显然,一个局部树结构导致最大协调数,而最大重叠对应于最小协调数。 因此,他们将超边密度定义为[86]:\[D_h(u)=\frac{Z_{max}(u)-Z(u)}{Z_{max}(u)-Z_{min}(u)} \quad ,\quad 0 \le D_h(u) \le 1 \quad \quad \quad (7)\] 资源和标签的超边密度定义是相同的。实证分析表明,这两个指标都表现出高聚类行为[82,86]。 协同标签网络超图的研究刚刚展开,如何正确量化聚类行为,节点之间的相关性和相似性以及社区结构仍然是一个开放的问题。
平均距离:定义为整个网络中两个随机节点之间的平均最短路径长度。
3. 推荐系统
推荐系统使用输入数据来预测其用户的潜在未来的喜好和兴趣。用户过去的评价通常是输入数据的重要组成部分。令\(M\)为用户数,令\(N\)为可评估和推荐的所有对象的数量。请注意,对象只是一个通用术语,可以表示书籍,电影或任何其他类型的消费内容。为了保持与标准术语的一致性,我们有时使用具有相同含义的词-“项目”。为了使符号更清楚,我们在枚举用户现在索引为拉丁字母 \(i\) 和 \(j\) ,以及枚举对象索引时限制为希腊字母 \(\alpha\) 和 \(\beta\)。用户 \(i\) 对对象 \(\alpha\) 的评价/打分表示为\(r_{i\alpha}\)。这个评估通常是以整数评分量表(比如亚马逊的五星级制)-在这种情况下,我们会认为是一个显明的评级。请注意,二进制评级(如/不喜欢或好/坏)的常见情况也属于此类别。当只存在收集对象(如在书签共享系统中)或简单地消费(如在没有评级系统的在线报纸或杂志),或者当“喜欢”是唯一可能的表达(如在Facebook上)时,我们只有一元评级。在这种情况下,\(r_{i\alpha}=1\) 表示收集/消耗/喜欢的对象,\(r_{i\alpha}=0\) 表示不存在的评估(参见图4)。推测用户对评级的置信区间是一个重要的工作,特别是对于二元或一元评级。用户的访问行为信息可能带来一些帮助,例如,可以通过观看电视节目的时间来估计用户的置信区间(喜好程度),并且借助于该信息,可以提高推荐质量[95]。即使我们有明确的评级,这并不意味着我们知道用户如何并为什么做出这样的打分-他们是否具有数值上的评分标准,或者只是使用其来表现排序?最近的证据[96]在一定程度上是支持后者的。
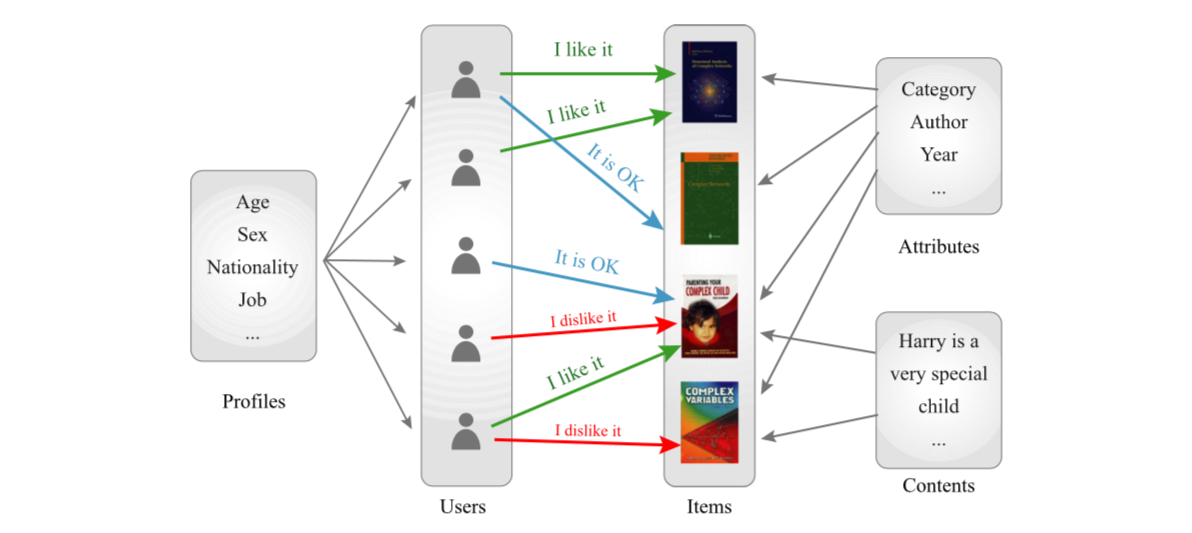 图4. 由五个用户和四本书组成的推荐系统的图示。 每个推荐系统包含的用户和对象之间的基本信息都可以由二部图来表示。 该图还展示了在推荐算法的设计中经常被利用的一些附加信息,包括用户信息,对象的属性和对象内容。
图4. 由五个用户和四本书组成的推荐系统的图示。 每个推荐系统包含的用户和对象之间的基本信息都可以由二部图来表示。 该图还展示了在推荐算法的设计中经常被利用的一些附加信息,包括用户信息,对象的属性和对象内容。
推荐系统的目标是为用户提供个性化的“推荐”对象。 因此,可以对那些用户不知道的对象预测用户的评价或者是计算推荐分数。 被预测为高评价或高推荐分数的对象便构成了呈现给目标用户的推荐列表。 推荐系统有着广泛的性能指标体系(见第3.4节)。 推荐系统的惯用分类如下[15]:
- 基于内容的推荐:推荐的对象是内容类似于目标用户先前喜欢的对象内容的对象。 我们在4.2.3节叙述。
- 协同推荐:根据大量用户过去的评估,选择推荐对象。 在表2中给出一个例子。它们可以分为:
- 基于记忆的协同过滤:推荐对象来自于与目标用户有相似偏好的用户喜欢的(user-base),或者是和目标用户之前喜欢的对象相似的对象(item-base)。我们将在第四章节(标准的基于相似的方法)和第七章节(引入社交网络的方法)来具体的阐述。
- 基于模型的协同过滤:推荐对象选自训练好的识别输入数据的模式的模型,我们将在第五章(降维方法)和第六章(基于信息传播理论的方法)具体来阐述。
- 混合方法:这类算法通过结合协同方法和基于内容的方法或者是混合多种不同的协同方法。我们将在8.4章节来具体的阐述
4. 推荐系统评估指标
其实可以参考看 2012 吕琳媛 推荐系统评价指标综述
给定目标用户\(i\),推荐系统将对所有\(i\)未收集的对象进行排序,并推荐排名最高的对象。 为了评估推荐算法,数据通常分为两部分:训练集\(E^T\)和测试组\(E^P\)。 训练集被视为已知信息,但是不允许使用来自测试组的信息来推荐。在本节中,我们简要回顾了用于衡量推荐质量的基本指标。如何选择特定指标(或指标)来评估推荐性能,这取决于系统应该实现的目标。当然,任何推荐系统的最终评估是由用户的判断决定的。
- 精度指标类
评分精度指标: 推荐系统的主要目的是预测用户未来的喜好和兴趣。 存在许多指标来评估推荐的各个方面性能。 两个著名的指标:均值绝对误差(MAE)和均方根误差(RMSE)用于测量预测评分与真实评分的接近程度。 如果$ r_{i}$ 是用户\(i\) 对对象 \(α\) 的真实评分,则\(\widetilde r_{i\alpha}\) 是预测的评分,\(E^P\)是隐藏的用户商品评分的集合,MAE和RMSE被定义为\[MAE = \frac{1}{|E^p|} \sum_{(i,\alpha)\in E^p} |r_{i\alpha} - \widetilde r_{i\alpha}| \quad \quad \quad (8) \] \[RMSE = \lgroup \frac{1}{|E^p|} \sum_{(i,\alpha)\in E^p} (r_{i\alpha} - \widetilde r_{i\alpha})^2 \rgroup ^{1/2} \quad \quad \quad (9) \] 较低的MAE和RMSE对意味着较高的预测精度。 由于RMSE在求和之前对误差进行平方,所以往往会更大程度地惩罚大错误。 由于这些指标平等对待所有评分,无论他们在推荐列表中的位置如何,所以它们对于某些常见任务,如找到可能被用户偏好的的少量对象(Finding Good Objects)来说并不是最佳的。 然而,由于其简单性,RMSE和MAE被广泛用于推荐系统的评估。
评级和排名相关性: 评估预测精度的另一种方法是计算预测值和真实值之间的相关性。 有三个着名的相关性测度,即皮尔逊相关系数(the Pearson product-moment correlation)[97],斯伯曼/斯皮尔曼相关系数 (the Spearman correlation)[98] 和 肯德尔相关系数(Kendall’s Tau )[99]。 Pearson相关性测量两组评分之间线性相关性的程度。它被定义为
\[PCC = \frac{\sum_{a}(\widetilde r_{\alpha} - \bar{\widetilde r} )(r_\alpha - \bar r)}{\sqrt{\sum_\alpha(\widetilde r_{\alpha}- \bar{\widetilde r} )^2} {\sqrt{\sum_\alpha(r_\alpha - \bar r)^2}}}\]
其中\(r_\alpha\) 和 \(\widetilde r_\alpha\) 分布死真实的和预测的评分。Spearman相关系数 \(\rho\) 以与Pearson相同的方式定义,除了\(r_\alpha\) 和\(\widetilde r_\alpha\) 被各个对象的排序代替。与Spearman相似,Kendall也评估了评分排名一致性程度。它被定义为 \(\tau = (C-D)/(C+D)\)其中C是系统以正确的排序顺序预测的对象的数量,D是系统以错误的顺序预测的不一致的数量。当真实和预测的排名相同时,\(\tau = 1\),当它们完全相反时,\(\tau = -1\)。 当真实排名或预测排名有并列情况出现时,在[13]中提出了Kendall的的变体, \[\tau = \frac {(C-D)}{\sqrt{(C+D+S_T)(C+D+S_P)}}\]其中\(S_T\)是真实评分中相同的对象的数量,\(S_P\)是预测评分相同的对象的数量。Kendall 指标对连续有序对象的任何位置交换给予相等的权重,无论它在哪里发生。 但是,不同地点的交换,例如在1号到2号之间,100到101号之间的交换可能会有不同的影响。 因此,可以对真实排名的顶部给予对象更大的权重来改进指标。与Kendall类似,最初由Yao[100]提出来的归一化基于距离的性能指标(NDPM)用来比较两种不同的弱排序,它是基于统计矛盾对\(C^-\)(2个排序不一致)和兼容对\(C^u\)(一个排序是平局,另外一个排序是在所有对象中明显偏向其中一个),值得注意的是,这些预测评分关联性指标都是只关注于预测排序值而不关注具体的预测评分值,所以它们都不适用于那些旨在为用户提供精确预测评分值的系统。假如用\(C\)表示用户实际评分中具有严格偏好差别的商品对个数,则NDMP指标定义为:\[NDPM=\frac{2C^-+C^u}{2C}\]
分类准确度: 分类指标适用于诸如“寻找好对象”这样的任务,特别是当仅有隐含评分可用时(即,我们知道哪些对象受到用户的青睐,而不是他们具体喜欢多少)。当给出排序的对象列表时,推荐的阈值是不明确的或可变的。为了评估这种系统,一个受欢迎的指标是AUC(Area ROC Curve),其中ROC代表接收者操作特征曲线[101](关于如何绘制ROC曲线见[13])。 AUC尝试测量推荐系统如何能够成功地将相关对象(用户所赞赏的)与无关对象(所有其他对象)区分开来。计算AUC的最简单方法是将相关对象推荐的概率与不相关对象的概率进行比较。对于n个独立比较(每个比较指的是选择一个相关的和一个不相关的对象),如果有\(n^\prime\)次相关对象分数高于不相关对象,\(n^{\prime\prime}\)次不相关对象和相关对象分数一致,根据[102]\[AUC=\frac{n^\prime+0.5n^{\prime\prime}}{n} \quad \quad \quad (13) \]如果所有的相关对象比不相关对象的分数高那么 \(AUC=1\),意味着一个完美的推荐系统。对于一个随机排序的推荐列表 \(AUC=0.5\),因此,AUC超过0.5的程度表示推荐算法识别相关对象的能力。类似于AUC是[103]中提出的所谓的排名分数。 对于给定的用户,我们测量该用户推荐列表中相关对象的相对排名:当有\(o\)个对象被推荐时,具有排名r的相关对象具有相对排名\(r/o\)。 通过对所有用户及其相关对象进行平均,我们获得平均排名得分RS-排名得分越小,算法的准确性越高,反之亦然。
由于真正的用户通常仅关注推荐列表的顶部,所以更实际的方法是考虑漂亮在top-L位置前用户相关的对象的数量。基于此,精准率和召回率是最受欢迎的指标。 对于目标用户\(i\),推荐的精确度和召回率$P_i(L) $ 和 \(R_i(L)\)被定义为\[P_i(L)=\frac{d_i(L)}{L} \quad , \quad R_i(L)=\frac{d_i(L)}{D_i} \quad \quad \quad (14)\]其中\(d_i(L)\)指在长度为L的推荐列表中相关的项目数量,\(D_i\)是所有的相关项目总数,对所有拥有至少一个相关对象的所有用户的精度和回召率做平均,我们可以得到平均精度和平均回召率\(P(L),R(L)\),这些指标可以通过对随机产生的推荐结果进行对比,于是就有了增强版本的精度和回召率指标\[e_P(L)=P(L)\frac{MN}{D} \quad , \quad e_R(L)=R(L)\frac{N}{L} \quad \quad \quad (15)\]其中\(M\)和\(N\)分别是用户和商品的数量,\(D\)是所有相关商品的数量,通常精度回随着推荐列表长度L增加而下降,召回率随着L的增加而增长,我们可以把他们组合成一个和L弱相关的指标\(F_1\)-score。\[F_1(L)=\frac{2PR}{P+R}\quad \quad \quad (16)\]许多其他组合精度和召回率的指标被用在信息检索的有效性,但是很少用在推荐系统中:平均精度,深度精度,R精度,互惠等级[106],二进制偏好度量[107]。 每个组合指数的详细介绍和讨论可以在[108]中找到。
- 基于排序加权的指标
现实生活中用户的耐心往往是有限的,一个人不太可能会不厌其烦地检查推荐列表中的所有商品,所以用户体验的满意度往往会受到用户喜欢的商品在推荐列表中位置的影响,这里介绍3个具有代表性的评价指标,更详细的信息参见文献[13]。
半衰期效用指标(half-life utility)[109] 是在用户浏览商品的概率与该商品在推荐列表中的具体排序值呈指数递减的假设下提出的,它度量的是推荐系统对一个用户的实用性也即是用户真实评分和系统默认评分值的差别。用户\(i\)的期望效用定义为:\[HL_i=\sum^n_\alpha\frac{max(r_{i\alpha}-d,0)}{2^{(o_{i\alpha}-1)/(h-1)}} \quad \quad \quad (17)\] 推荐结果按照数\(\widetilde r_{i\alpha}\)降序排列,\(r_{i\alpha}\)表示用户\(i\)对商品\(\alpha\)的实际评分,而\(o_{i\alpha}\)为商品\(\alpha\)在用户\(i\)的推荐列表中的排名;\(d\)为默认评分(如说平均评分值);\(h\)为系统的半衰期,也即是有50%的概率用户会浏览的推荐列表的位置。显然,当用户喜欢的商品都被放在推荐列表的前面时,该用户的半衰期效用指标达到最大值。通过计算有用户\(HL_i\)值的平均值,我们就得到了系统的整体效果。
折扣累计利润(discounted cumulative gain,DCG)[110] 对于长度为L的推荐列表,DGG定义为\[DGG(b) = \sum^b_n r_n+\sum^L_{n=b+1}\frac{r_n}{log_bn} \quad \quad \quad (18)\],其中\(r_n\)指排序中第n个项目的用户是否喜欢,\(r_n=1\)代表喜欢,\(r_n=0\)代表不喜欢,b是自由参数多设为2;DGG的主要思想是用户喜欢的商品被排在推荐列表前面比排在后面会更大程度上增加用户体验。
排序偏差准确率(Rank-biased precision)[108] 这个指标假设用户往往先浏览排在推荐列表的首位商品然后依次以概率\(p\)浏览下一个,以\(1-p\)的概率不再看此推荐列表。对于一个长队为L的推荐来说,RBP定义为\[RBP=(1-p)\sum^L_{n=1}r_nP^{n-1} \quad \quad \quad (19)\]其中\(r_n\)和DCG相同,RBP和DCG类似,唯一的不同在于RBP把推荐列表中商品的浏览概率按等比数列递减,而DCG则是按照log调和级数形式。
- 多样性和新奇
即便给用户成功推荐一个用户喜欢的项目,但是当项目是众人皆知(流行的)对用户来说的价值也是微乎其微。为了补充上面精度指标,几种多样性和新颖性指标 [35,39,111]在最近被提出,我在这里做一个介绍。
多样性 推荐系统的多样性是指被推荐项目之间的差异程度,在推荐系统中,多样性体现在以下两个层次,用户间的多样性(inter-user diversity),衡量推荐系统对不同用户推荐不同商品的能力;另一个是用户内的多样性(intra-user diversity),衡量推荐系统对一个用户推荐商品的多样性。用户间的多样性通过考虑用户推荐列表的种类来定义。对于用户i,j,可以用汉明距离来评估推荐列表的前L个项目差异性。\[H_{ij}=1 - \frac{Q_{ij}(L)}{L} \quad \quad \quad (20)\]其中\(Q_{ij}(L)\)是用户\(i,j\)之间前\(L\)个推荐商品中相同商品的数量,如果2个列表完全一致\(Q_{ij}(L)=0\),如果没有任何重叠则为\(Q_{ij}(L)=1\)。所有用户对的\(H_{ij}\)值的平均值就是系统的\(H(L)\)值,该值越大,则推荐系统给用户推荐的多样性越好
将用户\(i\)的推荐商品表示为\(\{o_1,o_2,...,o_L\}\),可以使用这些商品的相似度\((o_\alpha,o_\beta)\)来测量用户内多样性(这种相似性可以直接从评分或对象元数据获取)[113]。 用户\(i\)推荐商品的平均相似度,\[I_i(L)=\frac{1}{L(L-1)} \sum_{\alpha \neq \beta } s(o_\alpha,o_\beta) \quad \quad \quad (21)\],同样,我们可以通过平均所有用户值来获得系统的用户内的多样性值\(I(L)\),该值越小说明用户内的多样性越好。值得注意的是,通过避免推荐过度相似的对象,用户内推荐列表多样性可用于增强和改进推荐列表[37]。 可以通过在推荐列表[111]中引入对象排名的折扣函数来获得等级敏感版本。通过引入关于商品排序的折扣函数就可以获得排序敏感的版本(The rank-sensitive version can be obtained by introducing a discount function of the object’s rank in recommendation list [111].)[111]。
新颖性和惊喜性 推荐系统中的新颖性是指推荐对象与用户以前看过的不同之处。 量化算法产生新颖和意想不到的结果的能力的最简单的方法是测量推荐对象的平均受欢迎程度\[N(L)=\frac{1}{ML}\sum^m_{i =1}\sum_{\alpha \in O^i_R}K_\alpha \quad \quad \quad (22)\]其中\(O^i_R\)是用户\(i\)的推荐列表,\(K_\alpha\)是商品\(\alpha\)的度(商品的流行性),低流行性意味着推荐结果的高新颖性。另外一个可以用来评估推荐结果的惊喜性的指标通过计算自信息(self-information)[114]。对于一个商品\(\alpha\),一个随机选取的用户选到他的概率为$k_/ M $,所以自信息定义为 \[U_\alpha = \log_2(M/K_\alpha) \quad \quad \quad (23)\]可以通过将观察限制到目标用户,即计算目标用户的top-L商品的平均自我信息来定义基于用户相关的新颖性指标变体。对所有用户进行平均,我们获得了平均top-L惊喜值\(U(L)\)。通过类似的结果公式,在[111]中提出了一种基于发现的新颖性,通过考虑对象是随机用户已知或熟悉的概率。
- 覆盖率
覆盖率指标是指算法向用户推荐的商品能够覆盖全部商品的比例。将所有推荐列表的前L个位置中的不同对象的总数表示为\(N_d\),则\(L\)相关的覆盖率指标定义为\[COV(L)=N_d/N\]低覆盖率表示该算法可以访问并仅推荐少量不同对象(通常是最受欢迎的),这往往导致很少的不同商品。相反,覆盖率较高的算法更有可能提供不同的推荐[115]。从这个观点来看,覆盖率也可以被认为是一种多样性度量。此外,覆盖率有助于更好地评估精度指标的结果[116]:推荐流行的对象可能具有高精度但低覆盖率。一个好的推荐算法应该将同时具有高精度和覆盖率。
评估推荐系统的特定指标的选取取决于系统需要实现的目标。在实践中,可以为新的和有经验的用户分别指定不同的目标,这进一步使评估过程复杂化。为了更好的概述,表3总结了推荐系统评估指标。
Table3. 推荐系统指标摘要。第三列表示度量的偏好(例如,更小的MAE意味着更高的评级精度)。第四列描述度量的范围。最后两列显示该度量是否从排名获得,以及是否取决于推荐列表L的长度。
| 名字 | 符号 | 偏好 | 范围 | 是否与排名相关 | 是否依赖长度L |
|---|---|---|---|---|---|
| MAE | \(MAE\) | Small | Rating accuracy | No | No |
| RMSE | \(RMSE\) | Small | Rating accuracy | No | Yes |
| Pearson | \(PCC\) | Large | Rating correlation | No | No |
| Spearman | \(\rho\) | Large | Rating correlation | No | Yes |
| Kendall’s Tau | \(\tau\) | Large | Rating correlation | No | Yes |
| NDPM | \(NDPM\) | Small | Ranking correlation | No | Yes |
| Precision | \(P(L)\) | Large | Classification accuracy | Yes | Yes |
| Recall | \(R(L)\) | Large | Classification accuracy | No | Yes |
| F1-score | \(F1(L)\) | Large | Classification | Yes | Yes |
| AUC | \(AUC\) | Large | accuracy Classification | No | No |
| Ranking score | \(RS\) | Small | accuracy Ranking | Yes | Yes |
| Half-life utility | \(HL(L)\) | Large | accuracy Satisfaction | No | No |
| Discounted Cumulative Gain | \(DCG(b, L)\) | Large | Satisfaction and precision | No | Yes |
| Rank-biased Precision | \(RBP(p,L)\) | Large | Satisfaction and precision | Yes | No |
| Hamming distance | \(H(L)\) | Large | Inter-diversity | No | Yes |
| Intra-similarity | \(I(L)\) | Small | Intra-diversity | Yes | No |
| Popularity | \(N(L)\) | Small | Surprisal and novelty | No | Yes |
| Self-information | \(U(L)\) | Large | Unexpectedness | Yes | No |
| Coverag | \(COV(L)\) | Large | Coverage and diversity | No | Yes |