Lucene是什么
Lucene 是一个基于 Java 的全文信息检索工具包，它不是一个完整的搜索应用程序，而是为你的应用程序提供索引和搜索功能。Lucene 目前是 Apache Jakarta 家族中的一个开源项目。也是目前最为流行的基于 Java 开源全文检索工具包。
Lucene总的来说是：
- 一个高效的，可扩展的，全文检索库。
- 全部用Java实现，同时提供python接口（pylucene)。
- 仅支持纯文本文件的索引(Indexing)和搜索(Search)。
Lucene数学模型
文档，域(字段)，词元
文档是Lucene搜索和索引的原子单位，文档为包含一个或者多个域(字段)的容器，而域(字段)则是依次包含“真正的”被搜索的内容，域(字段)值通过分词技术处理，得到多个词元。
举个栗子，一篇小说（斗破苍穹）信息可以称为一个文档，小说信息又包含多个域(字段)，例如：标题（斗破苍穹）、作者、简介、最后更新时间等等，对标题这个域(字段)采用分词技术又可以得到一个或者多个词元（斗、破、苍、穹）。
Lucene检索过程
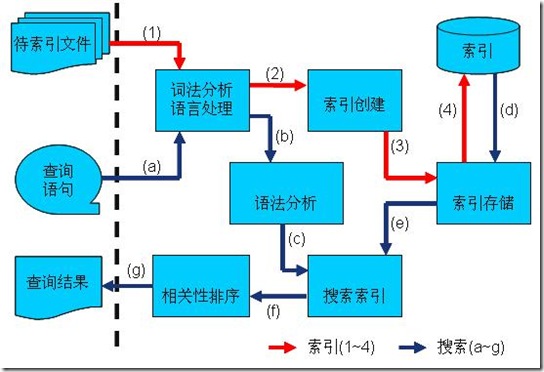
打分算法
BIR（布尔模型）
布尔逻辑将是建立最早的模型，也是目前应用最广泛的检索技术。它是通过布尔逻辑运算符：逻辑与（AND），逻辑或（OR），逻辑非（NOT）的组合来表达用户的检索需求。布尔逻辑是乔治·布尔在19 世纪中期定义的代数系统。1957 年，巴·希列尔最先探讨了将布尔逻辑应用到计算机检索的可能性。上世界 6，70 年代，布尔检索模型被正式用于各类文献系统并且逐步成为商业标准，这种模型并不提供任何的文档相关性测度，对于文档与查询的评价就只有“匹配”，“不匹配”两种而已，用户必须详细的规划自己的查询。
TF-IDF（词频-反词频）
本质上，TF-IDF通过确定特定文档中的单词的相对频率与该单词在整个文档语料库中的反比例相比较起作用。 直观地，该计算确定给定单词在特定文档中的相关性。 在一个单一或一小组文件中不常见的单词往往比普通单词（如冠词和介词）具有更高的TF-IDF值。不同的情景下实现的TF-IDF有一些微小不同的地方，但是总体上计算的方式如下： 给定一个稳定集合\(D\)，一个单词 \(w\) 和一个文档 \(d \in D\),我们计算\[\mathcal{W}_d=f_{w,d}*log(\frac{|D|}{f_{w,D}})\]其中 \(f_{w,d}\) 等于词 \(w\) 在文档 \(d\) 中出现的次数，\(|D|\)是文档全集的大小, \(f_{w,D}\) 是词 \(w\) 在全集中出现的次数(Salton & Buckley, 1988, Berger, et al, 2000)。假设\(|D|\thicksim f_{w,d}\),即语料库的大小大接近于\(w\)在集合\(D\)的频率，对于一些非常小的常数\(c\)，满足 \(1 < log(\frac{|D|}{f_{w,D}}) < c\) ,那么\(w\)将会比\(f_{w,d}\)小但是仍然是正的,这意味着\(w\)在整个语料库中比较常见，但在整个\(D\)句中仍然保持一定的重要性，例如TF-IDF在《新约》中的测试“Jesus”，就会是这种情况，与我们更加相关的例子在联合国文档的语料中“united”的结果可以预期到也是这种情况。对于非常常见的词语也是如此，例如冠词，代词和介词，它们本身在查询中没有任何相关的含义（除非用户明确要求含有这样的常用单词的文档）。 因此，这样的常用词得到非常低的TF-IDF分数，使得它们在搜索中基本上可以忽略不计。假设\(f_{w,d}\)非常大，\(f_{w,D}\)很小，那么\(log(\frac{|D|}{f_{w,D}})\)将会变得相当大，所以\(w_d\)同样会很大，因为具有高\(w_d\)的词意味着\(w\)是\(d\)中的重要词，而在\(D\)中不常见。这个词被认为具有很大的有辨识力的。
VSM（向量空间模型）
向量空间模型 (VSM：Vector Space Model) 是一个应用于信息过滤, 信息撷取, 索引以及评估相关性的代数模型。由Salton等人于60年代提出，并成功地应用于著名的SMART文本检索系统。文件(语料)被视为索引词(关键字)形成的多次元向量空间， 索引词的集合通常为文件中至少出现过一次的词组。在文本检索中，文档与查询词可以表示为以下向量空间模型[1] :\[d_j = (w_{1,j},w_{2,j},…,w_{t,j})\]\[
q = (w_{1,q},w_{2,q},…,w_{t,q})\]
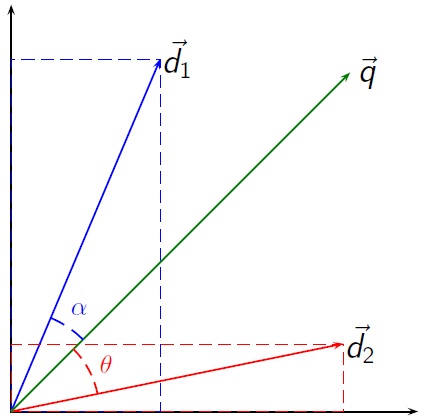
据文档相似度理论的假设，如要在一次关键词查询中计算各文档间的相关排序，只需比较每个文档向量和原先查询向量（跟文档向量的类型是相同的）之间的角度偏差。 实际上，计算向量之间夹角的余弦比直接计算夹角本身要简单。 \[{\displaystyle \cos {\theta }={\frac {\mathbf {d} \cdot \mathbf {q} }{\left\|\mathbf {d} \right\|\left\|\mathbf {q} \right\|}}}\] 其中 \({\displaystyle \mathbf {d_{2}} \cdot \mathbf {q} }\)是文档向量（即上 图中的d2）和查询向量（图中的q）的点乘。 \({\displaystyle \left\|\mathbf {d_{2}} \right\|}\)是向量d2的模，而 \({\displaystyle \left\|\mathbf {q} \right\|}\)是向量q的模。向量的模通过下面的公式来计算： \[{\displaystyle \left\|\mathbf {v} \right\|={\sqrt {\sum _{i=1}^{n}v_{i}^{2}}}}\] 由于这个模型所考虑的所有向量都是每个元素严格非负的，因此如果余弦值为零，则表示查询向量和文档向量是正交的，即不符合（换句话说，就是检索项在文档中没有找到）
Lucene打分模型
Lucene计算公式是对BIR，TF-IDF和vsm的一个综合使用和改进。首先采用BIR的方法把所有匹配的文档取出作为一个匹配文档集合，然后再用改进的VSM算法对这些文档进行排序，事实上由于Lucene是基于域的，所以的检索过程都是基于域的计算，最后按照域的权重求和得到最终的文档分数。VSM构建词向量的方式有很多种，其中比较有名的就是通过TF-IDF来构建，\(w_{i,j}\)通过计算文档\(d_j\)中\(i\)词在的TF-IDF值,虽然获得了词向量构建方法,但是会遇到查询\(q\)的维度远远小于文档\(d_j\)的问题，只需要以\(q\)的维度作为标准，文档\(d_j\)只在该基中映射。
按照原始的VSM模型，余弦的计算可以看做是2个归一化的向量内积，但是在实际应用中会遇到一些问题，显而易见的就是丢失了文档的长度信息，举个例子：
文档1：i think that 文档2：”I think it’s unlikely to be a real thing. I’m sure it’s an overreaction about an already-skittish party,” Roberts said. “They have looked at what happens in that circumstance.”, hello, i love the word. 查询“think”，那么按照原始的VSM返回的相似度是一样的。但是显然搜索的目的应该是偏向文档1的，为了解决这个问题，Lucene引入了一个和长度相关的归一化方法 \(f(\mathbf{d}_f)\) 所以改进后的VSM如下：\[{\displaystyle sim(\mathbf{q},\mathbf{d}_f)={\frac {\mathbf {q} \cdot \mathbf {d}_f }{\left\|\mathbf {q} \right\|}}}*f(\mathbf{d}_f)\] 接下来考虑一些更加定制化的内容：
- 我们可能会在系统中规定哪些文档是更加重要的，比如相对房地产平台销冠来说楼盘详细信息的文档就会比楼盘的小道消息重要，在查询楼盘的时候我们希望楼盘详细信息会出现在小道消息前面，我们可以通过给文档一个分数来定义文档的重要性计做\(w_{d}\)
- 同样的考虑到查询的关键字重要性定制化，我们引入查询权重向量计做\(\mathbf{w}_{q}\)
- Lucene是基于域的,所有的检索过程都是在域的尺度进行的，所以不同的域可以有相应的权重计做\(w_{f}\)
- 最后考虑到查询和域的匹配度，引入函数 \(f(\mathbf{q},\mathbf{d}_f)\) （关于查询向量\(\mathbf{q}\)和文档\(\mathbf{d}\) 域 \(f\) 向量的函数）
于是我们得到计算分数公式如下： \[sim(\mathbf{q}, \mathbf{d}) = w_d \cdot \sum_{f \in d}w_f \cdot sim(\mathbf{q},\mathbf{d}_f)\] \[sim(\mathbf{q},\mathbf{d}_f) = f(\mathbf{q},\mathbf{d}_f) \cdot ( \frac{(\mathbf{w}_{q}\circ\mathbf{q}) \bullet \mathbf{d}_f}{||(\mathbf{w}_{q}\circ\mathbf{q})||} \cdot f(\mathbf{d}_f)) \]
其中： > \(\circ\) 是“阿达马乘积”, > \(\bullet\) 是矩阵的“点积”, > \(\mathbf{q}\)是查询\(q\)词元的tf-idf单位向量, > \(\mathbf{d}_f\)是文档 \(d\) 的域 \(f\) 以向量\(\mathbf{q}\)为基的tf-idf值向量, > \(||\mathbf{q}||\)是向量\(\mathbf{q}\)欧几里德范数 > \(\mathbf{w}_q\)是向量\(\mathbf{q}\)中各个词元的权重向量
具体的 \[f(\mathbf{q},\mathbf{d}_f) = \frac{|\mathbf{q} \cap \mathbf{d}_f|}{|\mathbf{q}|}\]\[tf_{t,d} = f_{t,d} ^\frac{1}{2}\]\[idf_{t,d}= 1+ log(\frac{|D|+1}{f_{t,D}+1})\]\[f(\mathbf{d}_f) = t^{\frac{1}{2}} \cdot w_f\] 考虑到Lucene允许在同一个文档中写入多个同名的域，所以\[w_f = \prod w_{f,t} \]